ECE 147C - CONTROL SYSTEMS DESIGN PROJECT/
ME 155C - CONTROL SYSTEMS LABORATORY
Mo-We, 9:30- 10:45pm, Phelps 1444
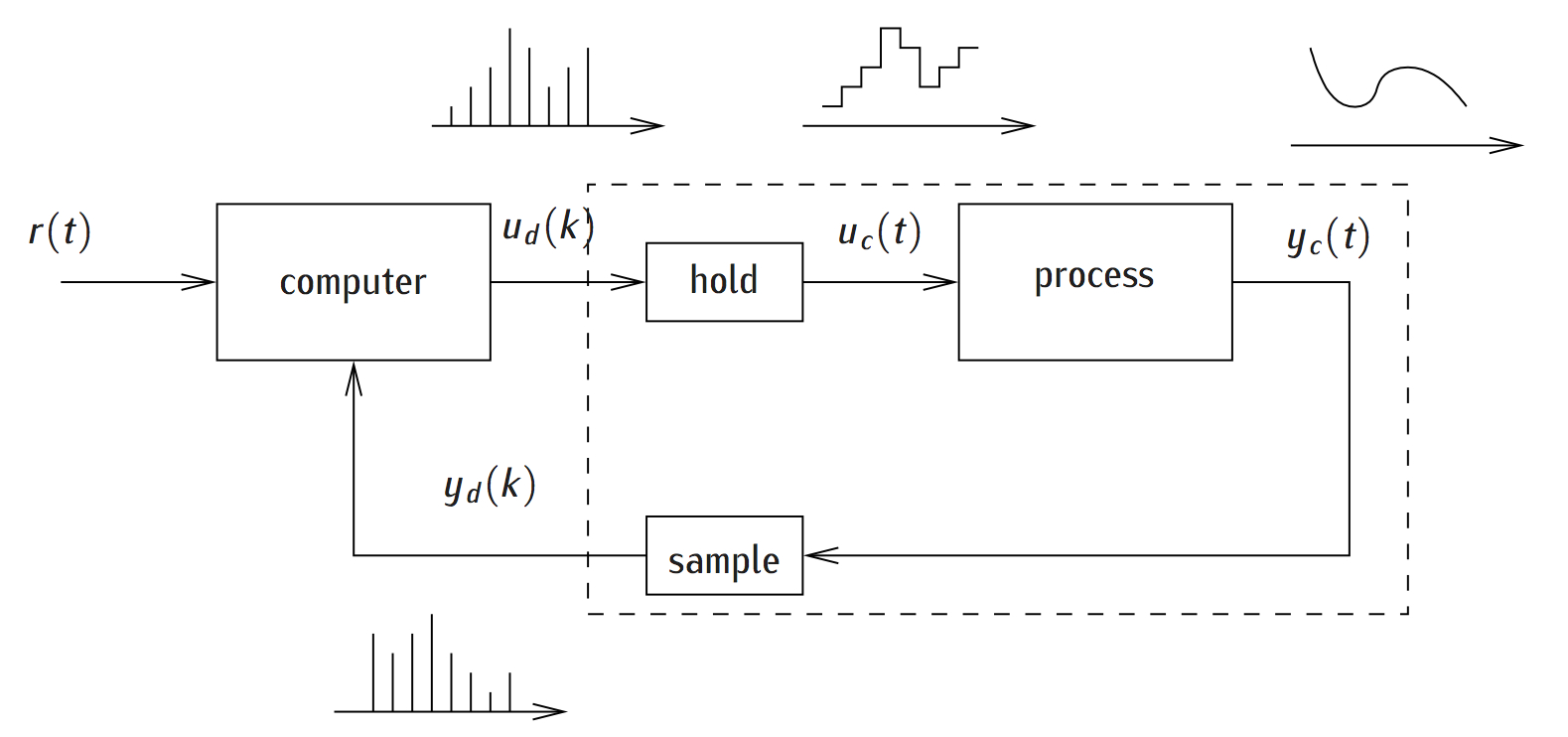
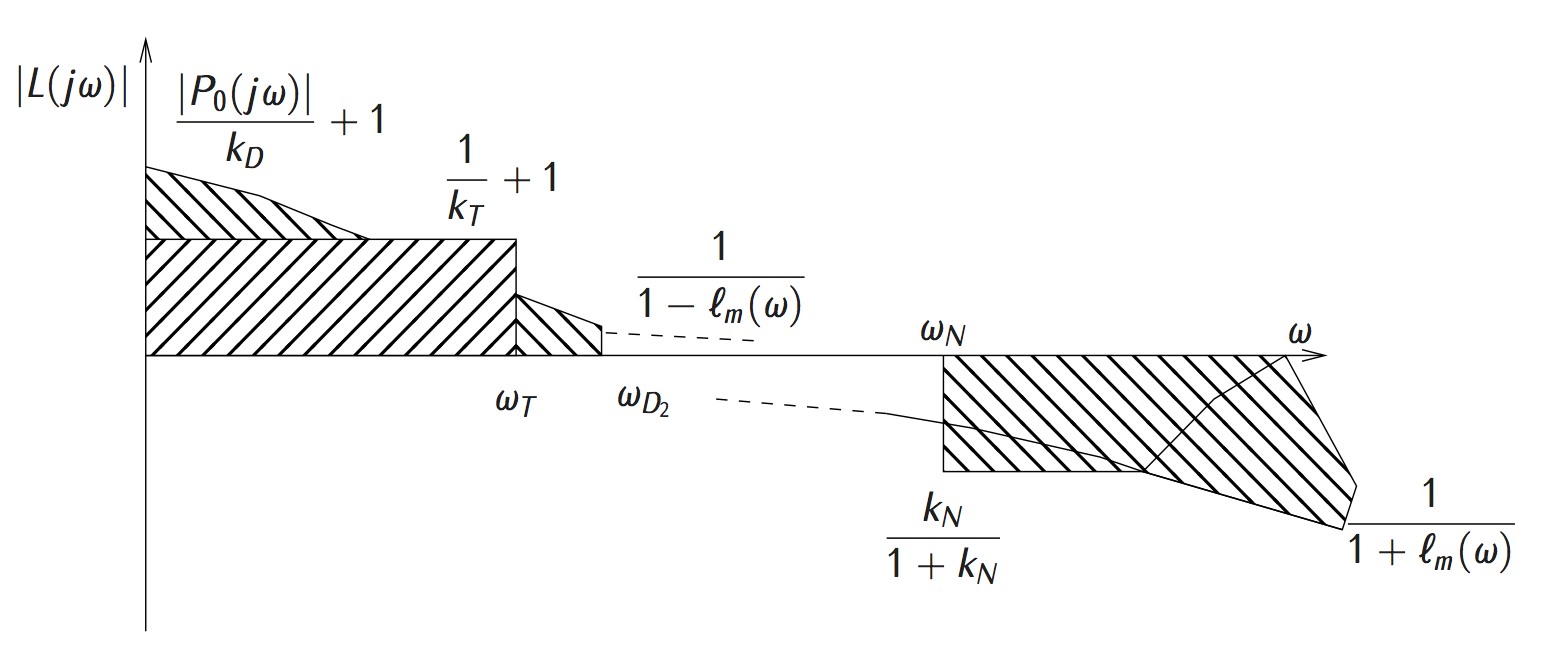
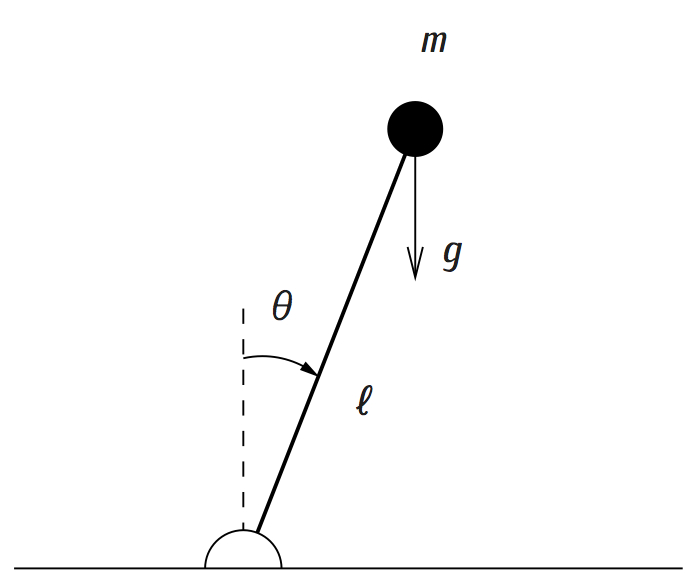
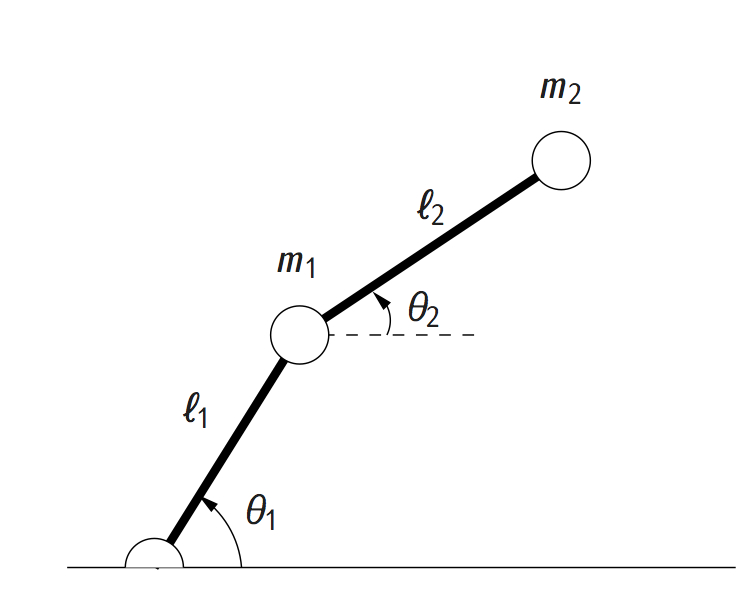
The objective of this course is to provide students with the necessary knowledge to design, implement, and document a control engineering project.
The course has three components: lectures, prepared laboratories (in the form of a project that is the same for all students), and a design project (specific to each group of students).
The lectures and laboratories cover a range of special topics related to the practical implementation of control systems that are not covered in introductory control courses but that are likely to arise in the professional career of controls engineers. These include:
- Model identification and parameter estimation (least-square identification of a auto-regressive model; nonparametric identification in the time domain; and nonparametric identification in the frequency domain)
- Robust Control (Nyquist-plots, small-gain, and passivity)
- Optimal control (LQR/LQG for state-space systems and time-optimal controller for the positioning of a mass using force actuation)
- Nonlinear control (Lyapunov's stability method; feedback linearization controller for a fully actuated 2nd order mechanical system; backstepping for triangular nonlinear systems; actuator limitations)
The course is heavily project-oriented and the students will be required to design, implement, document, and present a significant control systems project, which requires them to address the issues covered in the lectures. All laboratory work is done in groups of 2-3 students working together as teams that persist throughout the quarter.
Prerequisites
ECE147A or ME155A or equivalent. Open to all engineering majors.
Course's web page
All information relevant to the course will be continuously posted at the course's web page. The URL is
http://www.ece.ucsb.edu/~hespanha/ece147c-me155c/