grPartition.m
Status:
Pretty stable with a nice technical report to explain the algorithm. MATLAB’s
Statistics Toolbox is no longer required.
Download:
[tar file]
MATLAB function to partition very large graphs very fast. This function implements a graph partitioning algorithm based on spectral factorization. This algorithm is described in the following technical report:
João . An efficient MATLAB
Algorithm for Graph Partitioning. Technical Report,
This algorithm was extensively used in this paper:
C. Lim, S. Bohacek, J. , K. Obraczka. Hierarchical Max-Flow Routing. In Proc. of the IEEE GLOBECOM, Nov. 2005.
The script is used as follows:
% function [ndx,Pi,cost]=
grPartition(C,k,nrep);
%
% Partitions the n-node
undirected graph G defined by the matrix C
%
% Inputs:
% C - n by n edge-weights
matrix. In particular, c(i,j)=c(j,i) is equal
% to the cost associated with cuting the
edge between nodes i and j.
% This matrix should be symmetric and doubly
stochastic. If this
% is not the case, this matrix will be
normalized to
% satisfy these properties (with a warning).
% k - desired number of
partitions
% nrep - number of
repetion for the clustering algorithm
% (optional input, defaults to 1)
%
% Outputs:
% ndx - n-vector with the cluster index for every
node
% (indices from 1 to k)
% Pi - Projection matrix [see Technical report
% cost - cost of the
partition (sum of broken edges)
%
% By
%
% Example:
%
% X=rand(200,2); % place random points in the
plane
%
C=pdist(X,'euclidean'); % compute
distance between points
%
C=exp(-.1*squareform(C)); % edge cost
is a negative exponential of distance
%
% k=6; % # of partitions
% [ndx,Pi,cost]=
grPartition(C,k,30);
%
% colors=hsv(k); % plots points with appropriate
colors
% colormap(colors)
% cla
%
line(X(:,1),X(:,2),'MarkerEdgeColor',[0,0,0],'linestyle','none','marker','.');
% for i=1:k
% line(X(find(ndx==i),1),X(find(ndx==i),2),...
%
'MarkerEdgeColor',colors(i,:),'linestyle','none','marker','.');
% end
% title(sprintf('Cost
%g',cost))
% colorbar
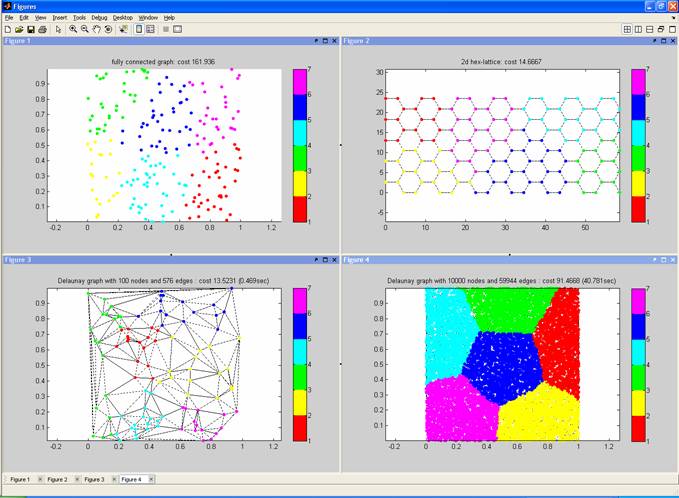
The following figures shows the output of the demo script ‘demo_grPartition.m’, which is included to illustrate the creation of several graphs. The top-left figure corresponds to the example above. The code that generated the remaining figures requires the @graph class available at http://www.ece.ucsb.edu/~hespanha/software.
The bottom-right figure demonstrates the speed of the algorithms for a large graph (10,000 nodes and about 60,000 edges). In my 2GHz PC, it took less than 1.5secc to create the graph and less than one minute to partition it. Since the costs are monotone functions of the Euclidean distance, one should not be too surprised to get a Voronoi-like partition of the space.
Bibliographic citation
When used in research, please acknowledge the use of this software with the following reference:
João Hespanha. grPartition — a MATLAB function for graph partitioning. Available at http://www.ece.ucsb.edu/~hespanha, Oct. 2004.
or if you use latex/bibtex:
@Misc{HespanhaOct04,
key =
{software},
author =
{Jo{\~a}o Pedro Hespanha},
title =
{\texttt{grPartition} a {MATLAB} function for graph partitioning},
howpublished = {Available at
\url{http://www.ece.ucsb.edu/~hespanha}},
month =
oct,
year =
2004
}
Disclaimer
This
program is free software; you can redistribute it and/or modify it under the
terms of the GNU General Public License as published by the Free Software
Foundation; either version 2 of the License, or (at your option) any later
version. This program is distributed in the hope that it will be useful, but
WITHOUT ANY WARRANTY; without even the implied warranty of MERCHANTABILITY or
FITNESS FOR A PARTICULAR PURPOSE. See
the GNU General Public License for more details (http://www.gnu.org/copyleft/gpl.html)