Summary of Our Approach
In this paper, we present a new foundation for counting a stationary crowd using a pair of WiFi transceivers. Consider a scenario such as the ones shown in Figure 1, where a number of people are seated. The people in the crowd are stationary, i.e., with no major body motion except breathing. However, people do not stay still for a long period of time and frequently engage in different kinds of small in-place natural body motions (called fidgets), such as adjusting their seating positions, crossing their legs, checking their phones, scratching, stretching, and coughing, among many others. We then show how the aggregate (collective) natural body fidgets of the crowd carry crucial information on the crowd count.
 |
Figure 1. Sample application scenarios of our stationary crowd counting system: (a) a group of people reading, (b) a group of people watching a movie, (c) attendance of a presentation, and (d) attendance of an event. |
Introducing the Aggregate Fidget Process
We define Crowd Fidgeting Periods (CFPs) as the time periods in which at least one person in the area is fidgeting, and Crowd Silent Periods (CSPs) as the periods in which no one in the area is fidgeting (i.e., everyone is only breathing). Figure 2 shows sample fidgeting processes of N people, the aggregate fidgeting process that results from the superposition of the individual processes, as well as the corresponding CFPs and CSPs. The aggregate fidget process and the corresponding CFPs and CSPs are easily extractable from the received WiFi signals. Intuitively, the more the number of people, the higher the chance that the CFPs are longer and the CSPs are shorter. Thus, these periods implicitly carry information on the total number of people. But how can we explicitly relate them to the total number of seated people in an area? That is what we show next.
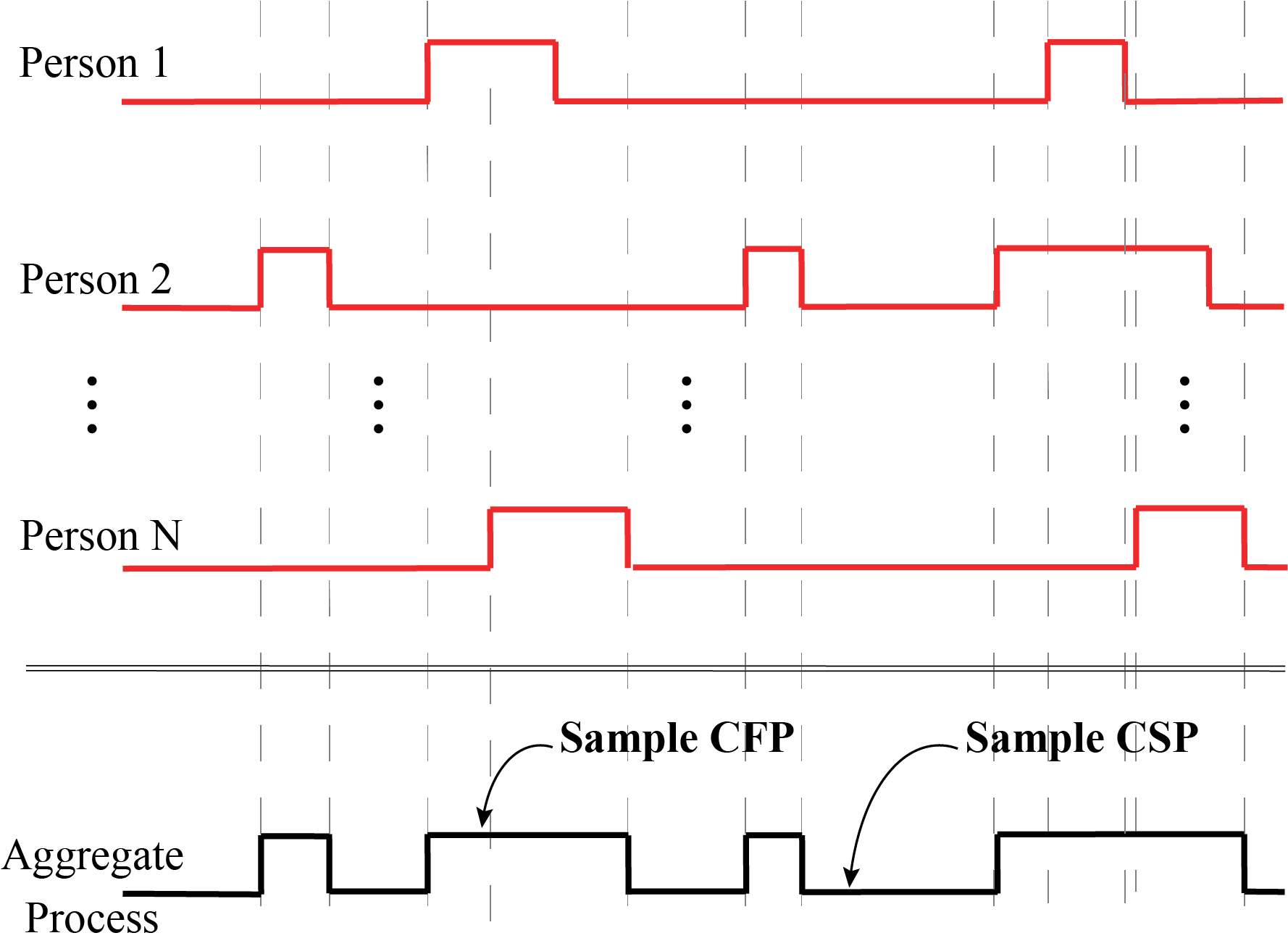 |
Figure 2. A sample fidgeting timeline of N people in an area, where a non-zero signal indicates a fidget. An aggregate fidgeting process results from the superposition of the individual fidgeting processes, where the state of no one fidgeting is referred to as the Crowd Silent Period (CSP), while the state of at least one person fidgeting is referred to as the Crowd Fidgeting Period (CFP). A sample CFP and CSP are marked on the figure. |
Similarity with Queuing Theory
We first reveal how this problem resembles a several-decade-old queuing theory problem, a seemingly-unrelated problem from a completely different field. Queuing theory is a branch of mathematics that studies waiting lines in systems that involve the arrival of customers. The customers require a service from an entity that includes a number of servers. Figure 3 shows an example of such a system. Considerable research has been conducted
in this area to characterize several quantities related to this problem,
such as the statistics of the waiting time of the customers, the
average number of customers waiting at any time instant, and other
related parameters.
 |
Figure 3. A sample queue with a number of servers and a number of customers. |
We then show how the CSPs are similar to the times when no customer is at a queue that has infinite servers, while the CFPs resemble the times when at least one customer is being served at such a queue. This then allows us to borrow mathematical tools from queuing theory to develop a completely new technique for counting the total number of stationary people.
More specifically, we show how our problem of mathematically modeling the statistics of the crowd fidgeting and silent periods can be posed similar to an M/G/∞ queuing theory problem. By borrowing and adapting mathematical tools from queuing theory, we can then characterize the aggregate crowd fidgeting dynamics and mathematically relate them to the total number of people. Figure 4 summarizes our main derivations
 |
Figure 4. Our main derivations for the relation between the crowd fidgeting statistics and the total number of people. |
Sample Experimental Results
We have run several experiments to validate the proposed framework. In these experiments, a crowd of up to and including 10 seated people is engaged in different kinds of activities, e.g., reading or watching a movie/documentary. Overall, our approach was able to count the number of people, with an error of 0 or 1 person, in 26 out of 27 experiments in non-through-wall scenarios (counting accuracy of 96.3%), and in 18 out of 20 experiments in through-wall scenarios (counting accuracy of 90%). We next show sample results.
Experiments in Area 1:
In these experiments, a pair of WiFi transceivers are placed in a cluttered patio area to count the number of people in the crowd, as shown in Figure 5. We carried out a total of 19 experiments in this area where up to and including 10 people gathered together to watch a movie. Our proposed framework was able to count the number of people (with a counting error of 0 or 1 person) in 18 out of the 19 experiments.
 |
| Figure 5. (a) Two sample experiments in the first test environment (Area 1): an outdoor patio with several sources of clutter, where up to and including 10 people gather to watch a movie. (b) Seating configuration for three sample experiments in Area 1, where (top) 10 people sit in a 4-4-2 configuration, (middle) 9 people sit in a 5-4 configuration, and (bottom) 6 people sit in a 6-0 configuration. (c) Counting results, as a function of time, for (left) an experiment with 10 people in a 4-4-2 configuration and (right) an experiment with 8 people in a 4-2-2 configuration. (d) Final counting results for all the 19 experiments conducted in Area 1, showing that in 94.7% of experiments, the counting error was 0 or 1. An n1-n2-n3 configuration refers to n1 people in the first row, n2 people in the second row, and n3 people in the third row. |
Experiments in Area 2:
In these experiments, a pair of WiFi transceivers are placed in an apartment, where a group of 4 people gather to watch a lecture, as illustrated in Figure 6. We carry out 4 experiments in this area where the participants are seated in different configurations. Our proposed framework was able to count the number of people (with a counting error of 0 or 1 person) in all experiments in this area.
 |
| Figure 6. (a) The second test environment (Area 2): four residents of an apartment gather in the living room to watch a lecture, in different seating configurations. (b) The floor plan of the apartment showing the locations of the Tx, the Rx, and the 4 participants sitting in a 2-2 configuration. (c) Estimation of the number of people for an experiment where the participants were seated in a 4-0 configuration. (d) The final counting results of the 4 experiments conducted in Area 2, showing a very good counting performance in an indoor environment (counting error of 0 or 1 in all experiments). |
Experiments in Area 3:
In these experiments, a pair of WiFi transceivers are placed near the entrance of a building (semi-open area), as illustrated in Figure 7. We carry out 4 experiments in this area where 8 or 10 people sit together in different seating configurations while reading. Our proposed framework was able to count the number of people (with a counting error of 0 or 1 person) in all experiments in this area.
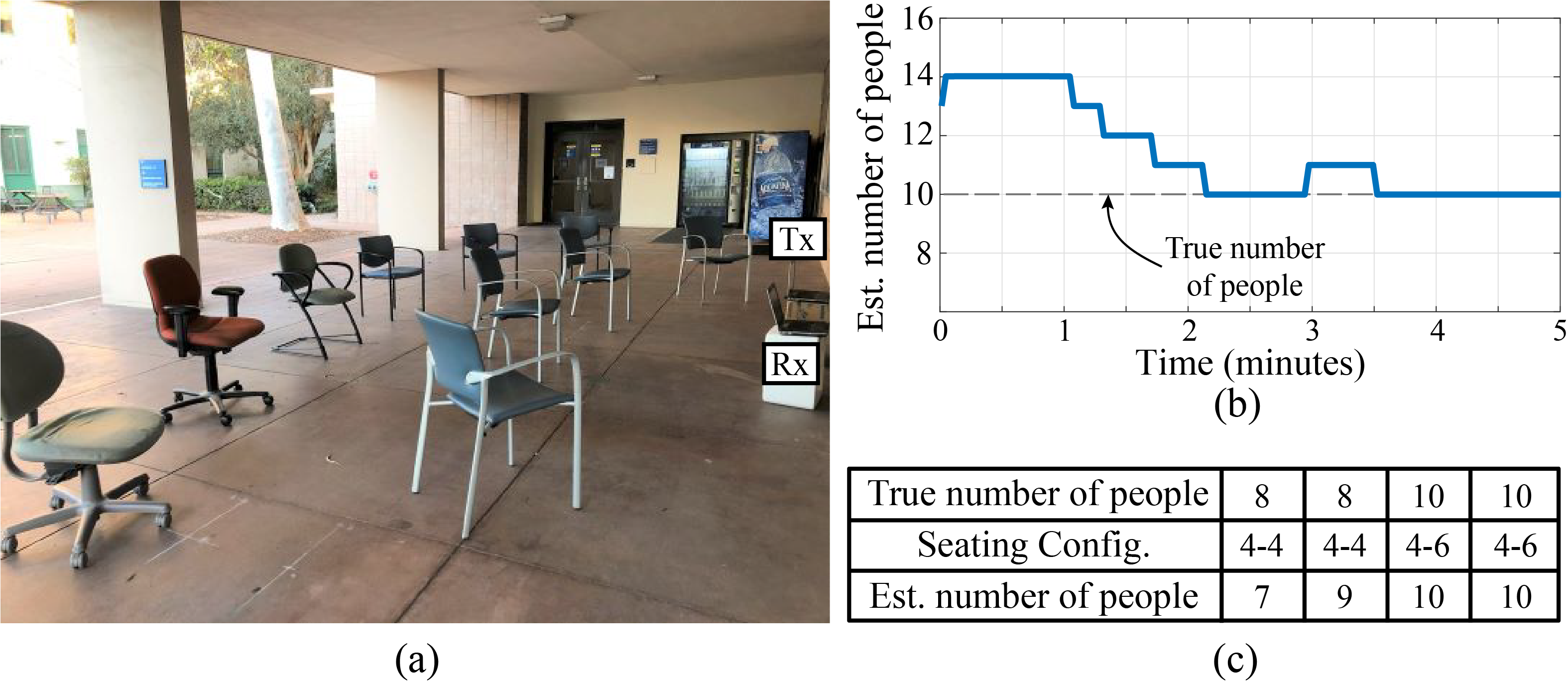 |
| Figure 7. (a) The third test environment (Area 3): a roofed space where 8 or 10 people are engaged in a reading activity. (b) Estimation of the number of people in one sample experiment in which 10 people sit in a 4-6 configuration. (c) The final counting results for all the 4 reading experiments in Area 3, showing a very good counting performance (counting error of 0 or 1 in all experiments). |
Experiments in Area 4 (Through-wall counting):
We have also tested our proposed approach extensively in a through-wall scenario, as illustrated in Figure 8. A pair of WiFi transceivers are placed behind a wall to count the number of people in the crowd. We carry out a total of 20 experiments in this setting, where up to and including 10 people sit together in different seating configurations and engage in different activities (e.g., reading or watching a documentary). Our proposed framework was able to count the number of people (with a counting error of 0 or 1 person) in 18 out of the 20 experiments in this area.
 |
| Figure 8. Through-wall crowd counting — (a) Two snapshots of sample experiments in the fourth test environment (Area 4): a roofed space where the Tx/Rx are placed behind a wall. (b) The final counting results for all the 20 experiments in Area 4 involving different activities (reading and watching a documentary), showing a very good counting performance in through-wall scenarios (counting error of 0 or 1 in 90% of experiments). |
Overall, our proposed framework was able to count the number of people (with an error of 0 or 1 person) in 26 out of 27 experiments in non-through-wall scenarios (counting accuracy of 96.3%), and in 18 out of 20 experiments in through-wall scenarios (counting accuracy of 90%).
Prior Work on Crowd Counting with WiFi
As mentioned, previous work on WiFi-based crowd counting has mainly relied on people to walk around in order to be counted, and cannot be used for counting a stationary seated crowd. Here are two sample past papers: paper 1, paper 2.
Acknowledgments
Chitra Karanam, for her valuable contribution to the paper.
All the students who participated in our experiments.