Summary of Our Approach
In this work, we present a new foundation for imaging still objects with only WiFi power measurements of a 2D grid of COTS receivers. Consider the scenario shown in Fig. 1, where a fixed wireless transmitter (located at \(\mathbf{p}_t \in \mathbb{R}^3\)) emits radio signals which interact with a set of objects located at \(\mathbf{p}_o \in \Theta \subset \Psi\), where \(\Theta\) is the set of all object locations and \(\Psi\) is our imaging space of interest. The signals scattered from these objects are then captured by a uniform two-dimensional RX grid.
 |
Figure 1. Sample imaging scenario: a transmitter emits wireless signals, while a receiver grid makes received power measurements in order to image objects in \(\Psi\). |
Keller Cones: The Interaction of Wireless Signals with Edges
As discussed earlier, when a wave is incident on an edge point, i.e., a point of discontinuity on the object's surface normal direction, a cone of outgoing rays emerge according to Keller's Geometrical Theory of Diffraction (GTD). The angle of the cone is equal to the angle between the incident ray and the edge (which is also the axis of the cone). These diffraction cones are also known in the electromagnetic theory as Keller cones. Note that this interaction is not limited to visibly sharp edges but applies to a broader set of surfaces with a small enough curvature.
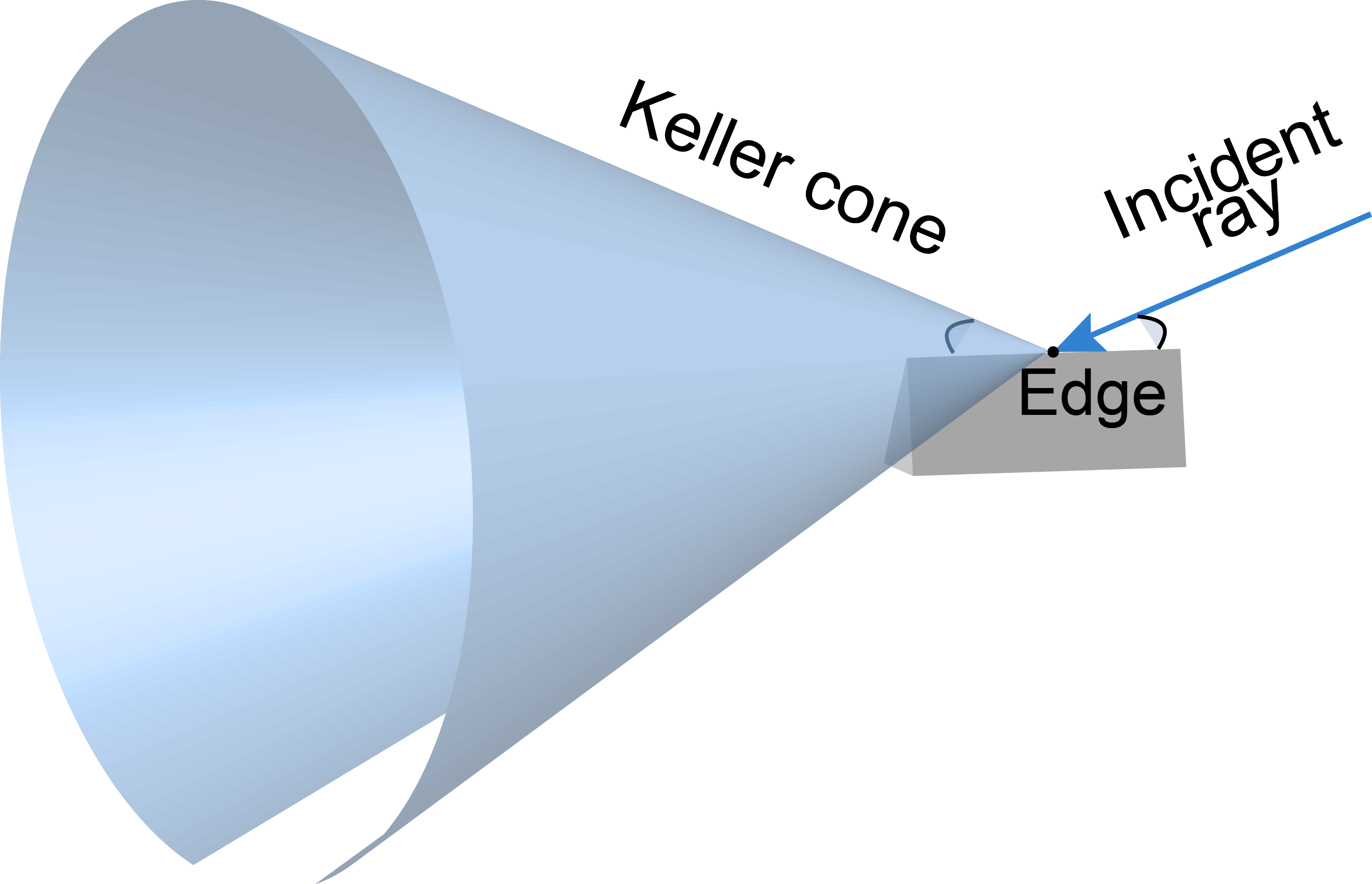 |
Figure 2. A sample edge interaction and the resulting Keller cone. |
If we consider a receiver grid in the vicinity of the edge, the edge leaves different signatures on the grid depending on its orientation and the direction of the incident ray. More specifically, the RX array elements at the intersection of the RX plane and the corresponding cone are the ones that receive the signal power and thus "see" the impact of that edge point. The intersection of the Keller cone with the RX plane will result in different 2-D shapes (e.g., hyperbola, ellipse, circle, etc.), formally referred to as conic sections.
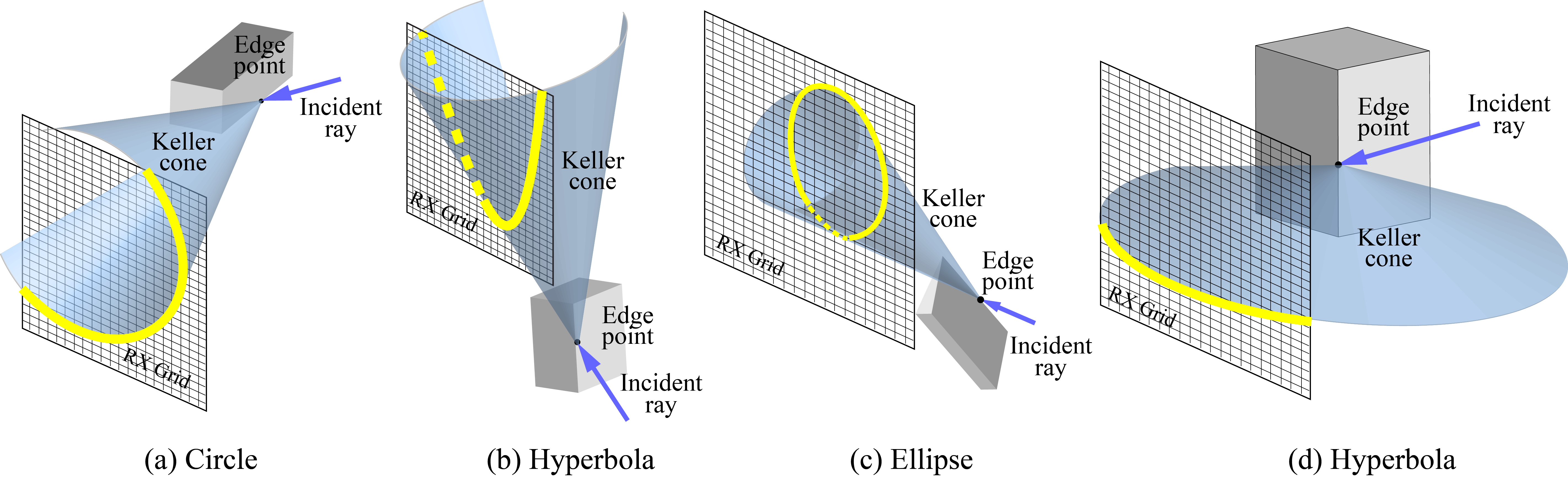 |
Figure 3. Diffracted rays off of edges with different orientations. Depending on the orientation of the edge and the direction of the incident wave, the diffracted rays leave different footprints on the RX grid, i.e., different conic sections (yellow). |
Keller-cone-based imaging kernels and edge-based hypothesis testing
We first derive the following approximation for the received CSI signal power on the RX grid, \[\bar{P}(\mathbf{p}_r) \approx 2\text{Re} \left\{\sum_{\mathbf{p}_o \in \Theta} \Lambda(\mathbf{p}_o, \mathbf{p}_t, \mathbf{p}_r) g^*(\mathbf{p}_t, \mathbf{p}_r) g(\mathbf{p}_o, \mathbf{p}_r) \right\},\] where \(\Lambda(\mathbf{p}_o, \mathbf{p}_t, \mathbf{p}_r)\) is the complex-valued amplitude attenuation and \(g(\mathbf{p}_i, \mathbf{p}_j)\) is the corresponding Green's function given by \(g(\mathbf{p}_i, \mathbf{p}_j) = e^{-j\frac{2\pi}{\lambda}||\mathbf{p}_i - \mathbf{p}_j||}\) . We then propose the following edge-based imaging kernel: \[\mathcal{I}(\mathbf{p}_m, \phi_i) = \Bigg| \sum_{\mathbf{p}_r \in RX} \!\!\!\!\bar{P}(\mathbf{p}_r)g(\mathbf{p}_t, \mathbf{p}_r)g^*(\mathbf{p}_m, \mathbf{p}_r) \mathbb{1}_{\mathbf{p}_r \in RX_{\mathbf{p}_m, \phi_i}} \Bigg|\nonumber\] where \(\mathbb{1}_{\mathbf{p}_r \in RX_{\mathbf{p}_m, \phi_i}}\) is the indicator function over the footprint of the edge on the RX grid denoted by \(RX_{\mathbf{p}_m, \phi_i}\), \(\mathbf{p}_m\) is the location of the edge and \(\phi_i\) is its corresponding angle. This kernel is implicitly a function of the edge orientations, a relationship we exploit to infer the existence/orientation of the edges via hypothesis testing over a small set of possible edge orientations \(\Phi\). In other words, the edge orientation that best matches the resulting Keller-cone-based signature (judged based on the value of the imaging kernel) is chosen for a given point \(\mathbf{p}_m\) that we are interested in imaging: \[\phi^\star(\mathbf{p}_m) = \operatorname*{arg\,max}_{\phi_i \in \Phi}\ \ \mathcal{I}(\mathbf{p}_m, \phi_i) \nonumber\] Bayesian Information Propagation
Edges of real-life objects have local dependencies. We then model the imaging space as a graph. Once we find the high-confidence edge points via the proposed imaging kernel, we then propagate their information to the rest of the points using Bayesian information propagation. This can further improve the imaging quality, since some of the edges may be in a blind region or may be overpowered by other edges that are closer to the transmitters. Applying image improvement tools from the area of vision
Finally, once an image is formed, we can further improve it by using image completion/classification pipelines from the area of vision. We note that traditional imaging techniques result in poor imaging quality, when deployed with commodity WiFi transceivers as the surfaces can appear near-specular at lower frequencies, thus not leaving enough signature on the receiver grid.
Sample Experimental Results
We now present experimental results for Wiffract by imaging several objects in three different areas, including through-wall scenarios. We take developing a WiFi Reader as one example application to showcase the capabilities of our proposed pipeline since it is a considerably challenging task that was not possible before, to the best of our knowledge. In addition to imaging several letters in non-through-wall settings, we further show how WiFi can read the letters of the word "BELIEVE" through walls. We put 6 omnidirectional WiFi antennas of two laptops on a Styrofoam tower, which is then mounted on an unmanned ground vehicle to synthesize a 2D grid of receivers as shown in the figure below. The NEMA23 motor on top of the Styrofoam tower enables vertical stepping whereas the ground vehicle's movement enables horizontal scanning, thus enabling synthesizing a 2D RX grid together. The scene is illuminated by three antennas of one WiFi card, as shown in Fig. 4. |
Figure 4. Sample experimental setup showing imaging through walls -- 6 antennas of two laptops serve as receivers while a WiFi card of one laptop is used for transmission. A vertical Styrofoam tower carrying the RX antennas is mounted on a ground robot to synthesize an RX grid in the x-z plane, on which we measure WiFi CSI power measurements from three TX antennas (of one WiFi card) simultaneously. |
We carried out extensive experiments in three different areas, shown in Fig. 5. Area 1 is an open area from all four sides, while Area 2 is open from two sides, with the other sides having pillars, walls and other objects. Area 3 is a cluttered and roofed entrance of a building, which we have used extensively for through-wall experiments.
 |
Figure 5. Experiment areas and sample objects. Outlines of objects are highlighted with dashed lines for better display. |
Experiments in Areas 1 and 2:
We ran 30 experiments for imaging uppercase English letters in Areas 1 and 2. Fig. 6 shows the final edge images for 14 sample experiments. The ground truth letters are also plotted for comparison. As can be seen, our approach can image the details of the letters pretty well. |
Figure 6. Our final results for imaging 14 sample letter-shaped objects with WiFi signals. The dashed lines represent the ground-truth while the solid lines represent our image. Each imaging plane is 1.4m \(\times\) 1.4m, as marked for the first letter. It can be seen that the details of the objects are imaged well. |
Experiments in Area 3:
We next show how our proposed approach can enable WiFi to image and further read through walls. More specifically, consider Area 3 of Fig. 6. We have placed the letters of the word "BELIEVE" behind the wall (one by one) for WiFi to read. Fig. 7 shows our final imaging results for this word. As can be seen, the word is imaged very well. Not only it is easy to identify the letters, but also the details of the letters are imaged well. Overall, Wiffract has enabled WiFi, for the first time, to read through walls. We have also imaged other objects. See the Publications for more details. |
 |
Figure 6. Through-wall reading: Our approach has enabled WiFi to image and read the letters of the word "BELIEVE" behind the wall of Area 3. The dashed lines represent the ground-truth while the solid lines represent our image. |
Prior Work
In 2009, our lab proposed an approach for enabling WiFi signals to sense and learn about the environment. Here are samples of our most recent work in the area of WiFi sensing: crowd analytics [PerCom 2018, MobiSys 2021], identifying a person from a sample video [MobiCom 2019], recognizing activities [Ubicomp 2020], smart health [IoT 2022], 3D through-wall imaging of still objects on drones [IPSN 2017], among other applications. High-quality imaging of still objects, however, is the most challenging application due to the lack of motion, which has motivated the new approach of this paper.Acknowledgments
National Science Foundation
Office of Naval Research