Menu:
Behrooz Parhami's ECE 252B Course Page for Spring 2025
Computer Arithmetic
Page last updated on 2025 June 17
Enrollment code: 12203
Prerequisite: ECE 154A (in lieu of ECE 152A and 152B)
Flipped class meetings: MW 12:00-1:00, Phelps 1431
Instructor: Professor Behrooz Parhami
Open office hours: MW 1:15-1:45, Phelps 1431
Course announcements: Listed in reverse chronological order
Course calendar: Schedule of lectures & other activities
Homework assignments: Four assignments, worth 40% in all
Exams: None for spring 2025
Research paper: Worth 60% of course grade
Research paper guidlines: Brief guide to format and contents
Poster presentation tips: Brief guide to format and structure
Policy on academic integrity: Please read very carefully
Grade stats: Grade range, mean, etc. for each activity
References: Textbook and other information sources
Lecture slides: Available on the textbook's Web page
Miscellaneous information: Motivation, catalog entry, history
Course Announcements
2025/06/17: The spring 2025 offering of ECE 252B (Computer Arithmetic) is officially over and course grades have been reported to the Registrar. Over the next few days, I will send each student a private e-mail message with his/her HW4 and research-paper grades, along with feedback on the research paper. Hope you have an enjoyable summer break!
2025/05/30: A Letter to my students: As we near the end of the 2024-2025 academic year, I want to congratulate you for another year of academic progress under difficult circumstances. The American system of higher education is under attack. An incompetent administration is gleefully cutting a tree that holds up our country’s social progress and economic prosperity. Many of you are experiencing uncertainties in sources of financial aid or academic salaries. Others are facing the prospects of visa revocation for their studies or practical training. As xenophobia spreads and anti-science officials take control of our government, the UC faculty and staff are doing everything in their power to protect you against shortsighted social and economic policies. Let’s maintain open lines of communication. We are in this together.
2025/05/21: HW4, the last one for the course, has been posted to the homework area below a few days ahead of schedule. We discussed FMA (fused multiply-add) and its speed & accuracy advantages in class today. This on-line article provides specific examples of these advantages for NVIDIA GPUs and their associated CUDA programming system.
2025/05/11: HW3 has been posted to the homework area below a day ahead of schedule.
2025/05/02: In the solutions handed out for HW2, problem 11.9 was mistakenly included in lieu of the assigned problem 11.1. The missing solution has been e-mailed to all students.
2025/04/19: HW2 has been posted to the homework area below a couple of days ahead of schedule.
2025/04/15: Please submit your HW solutions in hard-copy form. Research topics have been assigned to 17 students thus far. The assignments are reflected on the list of topics below. Please avoid choosing these 17 topics when submitting the list of your top 4 preferences.
2025/04/05: HW1 has been posted to the homework area below a couple of days ahead of schedule.
2025/02/09: Welcome to the Web page for the graduate course ECE 252B in spring 2025. Information on the spring 2024 and earlier offerings of the course is available under the "History" section at the end of this page. We will meet in flipped classes over the first hour of the scheduled time in Phelps 1431. The expectation is for students to have watched the recorded lecture associated with each class, in order to be able to engage in group discussion during our in-person meeting. Please watch this introductory video (ignoring references to Zoom meetings & office hours, as well as dates given for the spring 2021 offering) along with Lecture 1, before coming to the first class. The second hour of our scheduled class time has been converted to an open office hour for ECE 252B, ECE 1B, and other students. The office hours will be held in Phelps 1431, right after the flipped class. Throughout the current quarter, this "Course Announcements" section will alert you to significant additions or changes to this Web page. Please visit regularly.
Course Calendar
Course lectures, homework assignments, and research milestones have been scheduled as follows. This schedule will be strictly observed. Please review the first two chapters in the textbook (before the first class, if possible). These chapters contain material that you should already know. PowerPoint and pdf files of course lectures, including skipped material in Chapters 1-2, can be found on the textbook's web page. [Introductory video]
Day & Date (book chapters) Lecture/discussion topic [Homework posted/due] {Special notes}
M 03/31 (ch. 3) Redundant number representation {Lecture 1 (81 min.)}
W 04/02 (ch. 4) Residue number systems {Lecture 2 (74 min.)}
M 04/07 (Ch. 5) Basic addition and counting [HW1 posted] {Lecture 3 (69 min.)}
W 04/09 (ch. 6) Carry-lookahead adders {Lecture 4 (86 min.)}
M 04/14 (ch. 7) Variations in fast adders {Lecture 5 (91 min.)} {Research topic preferences}
W 04/16 (ch. 8) Multioperand addition [HW1 due] {Lecture 6 (85 min.)} {Research topics assigned}
M 04/21 (ch. 9) Basic multiplication schemes [HW2 posted] {Lecture 7 (66 min.)}
W 04/23 (ch. 10) High-radix multipliers {Lecture 8 (79 min.)}
M 04/28 (ch. 11) Tree and array multipliers {Lecture 9 (85 min.)}
W 04/30 (ch. 12) Variations in multipliers [HW2 due] {Lecture 10 (74 min.)}
M 05/05 (ch. 13) Basic division and some speedup methods {Lecture 11 (92 min.)}
W 05/07 (ch. 14) High-radix division {Lecture 12 (84 min.)} {Preliminary references due}
M 05/12 (ch. 15) Variations in dividers [HW3 posted] {Lecture 13 (65 min.)}
W 05/14 (ch. 16) Division by convergence {Lecture 14 (79 min.)}
M 05/19 (ch. 17) Floating-point number representation {Lecture 15 (86 min.)} {Abstract & ref's due}
W 05/21 (ch. 18) Floating-point operations [HW3 due] {Lecture 16 (75 min.)}
M 05/26 Memorial Day observance: No class session [HW4 posted]
W 05/28 (ch. 19-20) Errors, precision, and certifiability {Lecture 17 (82 min.)}
M 06/02 (ch. 21) Square-rooting methods {Lecture 18 (89 min.)}
W 06/04 (ch. 22-23) CORDIC algorithms and function evaluation [HW4 due] {Lecture 19 (84 min.)}
W 06/11 {Research paper due by midnight}
T 06/17 {Course grades due by midnight}
Homework Assignments
-Turn in your solutions in hard-copy form by the due date/time.
-Because solutions will be handed out on the due date, no extension can be granted.
-Include your name, course name, and assignment number at the top of the first page.
-Please ensure that your homework paper is clean & legible (handwritten work is okay).
-Although some cooperation is permitted, direct copying will have severe consequences
Homework 1: Number systems, addition/subtraction (ch. 1-7, due W 2024/04/16, 12:00 noon)
Do the following problems from the textbook: 1.1, 2.10, 3.4a, 4.19, 5.21, 6.13, 7.5
Homework 2: Multioperand addition, multiplication (ch. 8-11, due W 2024/04/30, 12:00 noon)
Do the following problems from the textbook: 8.8, 8.26, 9.4c, 9.14abc, 10.13, 11.1, 11.12
Homework 3: Variations in multiplication, division (ch. 12-16, due W 2024/05/21, 12:00 noon)
Do the following problems from the textbook: 12.12ab, 12.13ab, 13.12a, 13.21, 14.10, 15.6, 16.6
Homework 4: Floating-point arithmetic, square-rooting (ch. 17-21, due W 2024/06/04, 12:00 noon)
Do the following problems from the textbook: 17.2, 17.11, 18.6bc, 18.19, 19.23, 20.25, 21.2a
Sample Exams and Study Guide [Not applicable to spring 2025]
The following sample exams (from spring 2007 and 2008) are meant to indicate the types and levels of problems, rather than the coverage (which is outlined in the course calendar). Students are responsible for all sections and topics (in the textbook and class handouts) that are not explicitly excluded in the study guides that follow the sample exams, even if the material was not covered in class lectures.
Sample Midterm Exam (105 minutes)
Problem 1 [15 points] Defining concepts and terms. Define each of the following concepts/terms precisely and concisely within the space provided (about 1.5 inches per term) [3 points each]: Manchester carry chain; Multiplier recoding; ulp; Conditional-sum adder; Parallel prefix graph
Problem 2 [10 points] Number representation. Show that flipping (complementing) the sign bit of k-bit numbers in 2's-complement format results in biased representation and determine the bias amount that characterizes this new representation.
Problem 3 [20 points] Basic design concepts. Draw diagrams showing each of the following. No explanation is necessary; the diagrams should be self-explanatory.
a. How an ordinary binary adder can be augmented to perform addition or subtraction of 2's-complement numbers under the control of an add'/sub signal (0 means "add", 1 means "subtract").
b. How 2-bits-at-a-time or radix-4 sequential multiplication might be performed at high speed without Booth's recoding and without precomputing 3 times the multiplicand.
Problem 4 [15 points] Carry-skip addition.
a. Show that the optimal block width b in a fixed-block carry-skip adder is proportional to the square root of the word width k. [10 points]
b. Briefly discuss why carry-skip adders are of interest at all, given that faster logarithmic-time adders are available. [5 points]
Problem 5 [15 points] Multioperand addition. The following describes a multioperand addition process in tabular form:
0 0 8 8 8 8 8 8 8 8
0 2 6 6 6 6 6 6 6 4
0 4 4 4 4 4 4 4 3 2
1 3 3 3 3 3 3 3 2 1
2 2 2 2 2 2 2 2 1 1
a. Explain the process described by this table. [5 points]
b. In the hardware implementation implied by the table, what component types are used and how many of each? Be as precise as possible in specifying the components used. [10 points]
Problem 6 [25 points] Two's-complement multiplication.
a. Represent x = 3, y = −3, and z = 5 as 4-bit 2's-complement numbers. [5 points]
b. Using the right-shift algorithm, perform x times z, using the representations of part a, to get the 8-bit product p = 15. [10 points]
c. Using the left-shift algorithm, perform y times z, to get the 8-bit product p' = −15. [10 points]
Sample Final Exam (2.5 hours)
Do Problems 1-2, plus 5 of the remaining 6. If all optional problems are answered, the first 5 will be graded.
Problem 1 [15 points]
a. The standard 2-way carry operator has two pairs of inputs and a pair of outputs. Present a suitable generalization to an h-way operator with h pairs of inputs.
b. Name and justify one, and only one, advantage of each of the following dividers over the other two: high-radix, array, convergence.
c. Explain why square-rooting cannot be viewed as a special case of division, in the same way that squaring is a special case of multiplication.
Problem 2 [10 points] Problem 5.18c from the textbook.
Problem 3 [15 points] Problem 7.28 from the textbook.
Problem 4 [15 points] Problem 11.22 from the textbook.
Problem 5 [15 points] Problem 15.6 from the textbook.
Problem 6 [15 points] Problem 19.2 from the textbook.
Problem 7 [15 points] Problem 21.18 from the textbook.
Problem 8 [15 points] Problem 22.20abc from the textbook.
Midterm Exam Study Guide
The following textbook sections are excluded from the midterm exam: 3.4-3.6, 4.4-4.6, 6.3, 7.2, 10.5
Final Exam Study Guide
In addition to the midterm exclusions, the following textbook sections are excluded from the final exam covering Chapters 3-21: 15.4, 15.6, 19.4, 19.5, 19.6, 20.2, 21.4, 21.6
Research Paper and Presentation
Each student will review a subfield of computer arithmetic or do original research on a selected and approved topic. A list of research topics is provided below; however, students should feel free to propose their own topics for approval (include a brief description and a couple of references). A publishable report earns an "A" for the course, regardless of homework grades. See the course calendar for research milestones and due dates. Consult Research Paper Guidlines for formatting tips.
Topics for Part I of the Textbook: Number Representation
01. Implementation of Arithmetic Operations in Mechanical Calculators (Assigned to: Yu Jia)
D. E. Felt, Mechanical Arithmetic, or The History of Counting Machines, Washington Institute, 1916. [PDF]
S. Augarten, Bit by Bit: An Illustrated History of Computers, Ticknor & Fields, 1984.
Wikipedia, Arithmometer (First digital mechanical calculator strong and reliable enough to be used daily in an office environment)
G. C. Chase, "History of Mechanical Computing Machinery," IEEE Annals of the History of Computing, Vol. 2, No. 3, pp. 204-226, July 1980.
02. The Need for, and Practicality of, Decimal Computer Arithmetic in Hardware (Assigned to: )
E. M. Schwarz, J. S. Kapernick, and M. F. Cowlishaw, "Decimal Floating-Point Spport on the IBM System z10 Processor," IBM J. Research and Development, Vol. 53, No. 1, 2009.
L. K. Wang, M. A. Erle, C. Tsen, E. M. Schwarz, and M. J. Schulte, "A Survey of Hardware Designs for Decimal Arithmetic," IBM J. Research and Development, Vol. 54, No. 2, 2010.
03. Practical Implementations of Ternary Computer Arithmetic (Assigned to: )
04. A Comparison of Carry-Save and Borrow-Save Number Systems and Arithmetic (Assigned to: Zhaohongzhi Cai)
05. Modulo-(2a+1) Number Representations and Arithmetic (Assigned to: )
H. T. Vergos and C. Efstathiou, "Efficient Modulo 2n + 1 Adder Architectures," Integration, the VLSI J., Vol. 42, pp. 149-157, 2009.
G. Jaberipur and B. Parhami, "Unified Approach to the Design of Modulo-(2n±1) Adders Based on Signed-LSB Representation of Residues," Proc. 19th IEEE Int'l Symp. Computer Arithmetic, 2009.
06. Robust Residue Number Systems and Arithmetic (Assigned to: Guannan Wang)
B. Parhami, "Digital Arithmetic in Nature: Continuous-Digit RNS," The Computer J., Vol. 58, No. 5, pp. 1214-1223, May 2015.
L. Xiao, X.-G. Xia, and H. Huo, "Toward Robustness in Residue Number Systems," IEEE Trans. Signal Processing, Vol. 65, No. 6, pp. 1497-1510, March 2017.
07. Number Representation with Discrete Logarithms (Assigned to: )
A. Fit-Florea, L. Li, M. A. Thornton, and D. W. Matula, "A Discrete Logarithm Number System for Integer Arithmetic Modulo 2k: Algorithms and Lookup Structures," IEEE Trans. Computers, Vol. 58, No. 2, pp. 163-174, February 2009.
A. Joux, A. Odlyzko, and C. Pierrot, "The Past, Evolving Present, and Future of the Discrete Logarithm," Open Problems in Mathematics and Computational Science, pp. 5-36, 2014.
08. Arithmetic in the Human Brain (Assigned to: Jiaji Lu)
S. Cordes, C. R. Gallistel, R. Gelman, and P. Latham, P., "Nonverbal Arithmetic in Humans: Light from Noise," Perception & Psychophysics, Vol. 69, No. 7, pp. 1185-1203, 2007.
S. Dehaene, "The Neural Basis of the Weber-Fechner Law: A Logarithmic Mental Number Line," Trends in Cognitive Sciences, Vol. 7, No. 4, pp. 145-147, 2003.
A. Nieder and E. K. Miller, "Coding of Cognitive Magnitude: Compressed Scaling of Numerical Information in the Primate Prefrontal Cortex," Neuron, Vol. 37, pp. 149-157, 2003. {The mental number line seems to be logarithmic rather than linear.}
M. Piazza and S. Dehaene, "From Number Neurons to Mental Arithmetic: The Cognitive Neuroscience of Number Sense," The Cognitive Neurosciences, ed. by M. S. Gazzaniga, et al., pp. 865-77, 3rd ed., 2004.
R. Sarpeshkar, "Analog Versus Digital: Extrapolating from Electronics to Neurobiology," Neural Computation, Vol. 10, pp. 1601-1638, 1998.
Topics for Part II of the Textbook: Addition/Subtraction
09. Variable-Block Carry-Lookahead Adders (Assigned to: )
V. Kantabutra, "A Recursive Carry-Lookahead/Carry-Select Hybrid Adder," IEEE Trans. Computers, Vol. 43, No. 12, pp. 1495-1499, December 1993.
10. Parallel-Prefix Ling Adders (Assigned to: )
N. Burgess, "Implementation of Recursive Ling Adders in CMOS VLSI," Proc. 43rd Asilomar Conf. Signals, Systems, and Computers, November 2009, pp. 1777-1781.
11. Design of Optimal Adders with Input Timing Profile (Assigned to: Hsin Jung Hsieh)
12. Design of Approximate Adders for Speed and Energy Efficiency (Assigned to: )
R. Pathak, "A Review of Approximate Adders for Energy-Efficient Digital Signal Processing," Int'l Research J. Engineering and Technology, Vol. 5, No. 10, pp. 1895-1900, October 2018.
W. Ahmad, B. Ayrancioglu, and I. Hamzaoglu, "Low Error Efficient Approximate Adders for FPGAs," IEEE Access, Vol. 9, pp. 117232-117243, 2021.
13. Saturating Two-Operand and Multioperand Adders (Assigned to: Kelly Flippo)
G. A. Constantinides, P. Y. Cheung, and W. Luk, "Synthesis of Saturation Arithmetic Architectures," ACM Trans. Design Automation of Electronic Systems, Vol. 8, No. 3, pp. 334-354, 2003.
P. I. Balzola, M. J. Schulte, J. Ruan, J. Glossner, and E. Hokenek, "Design Alternatives for Parallel Saturating Multioperand Adders," Proc. IEEE Int'l Conf. Computer Design, 2001, pp. 172-177.
14. Saturating Parallel Counters and Compressors (Assigned to: Zeiler Randall-Reed)
15. Nonbinary Parallel Counters: The Ternary Example (Assigned to: )
M. De and B. P. Sinha, "Fast Parallel Algorithm for Ternary Multiplication Using Multivalued I2L Technology," IEEE Trans. Computers, Vol. 43, No. 5, pp. 603-607, May 1994.
16. Implementation of Parallel Counters Via Sorting Networks (Assigned to: Yuchen He)
S. W. A. H. Baddar and K. E. Batcher, Designing Sorting Networks: A New Paradigm, Springer, 2012.
R. Mueller, J. Teubner, and G. Alonso, "Sorting Networks on FPGAs," The VLDB J., Vol. 21, pp. 1-23, 2012.
17. Multiplexer-Based Designs for Parallel Counters and Compressors (Assigned to: )
W. Hong, R. Modugu, and M. Choi, "Efficient Online Self-Checking Modulo 2^n + 1 Multiplier Design," IEEE Trans. Computers, Vol. 60, No. 9, pp. 1354-1365, September 2011.
18. Counting Networks: Design Methods and Applications (Assigned to: )
J. Aspnes, M. Herlihy, and N. Shavit, "Counting Networks," J. ACM, Vol. 41, No. 5, pp. 1020-1048, 1994.
V. Sklyarov and I. Skliarova, "Design and Implementation of Counting Networks," Computing, Vol. 97, pp. 557-577, 2015.
Topics for Part III of the Textbook: Multiplication
19. Trade-offs in Compensation Methods for Truncated Multipliers (Assigned to: )
N. Petra, D. De Caro, V. Garofalo, E. Napoli, and A. G. M. Strollo, "Truncated Binary Multipliers with Variable Correction and Minimum Mean Square Error," IEEE Trans. Circuits and Sustems I, Vol. 57, No. 6, pp. 1312-1325, June 2010.
20. Truncated Squarers and Cubers (Assigned to: )
E. G. Walters, M. J. Schulte, and M. G. Arnold, "Truncated Squarers with Constant and Variable Correction," Advanced Signal Processing Algorithms, Architectures, and Implemenatations XIV (Proc. SPIE Conf. 5559), 2004, pp. 40-50.
N. Petra, D. De Caro, V. Garofalo, E. Napoli, and A. G. Strollo, "Truncated Squarer with Minimum Mean-Square Error," Microelectronics J., Vol. 45, No. 6, pp. 799-804, 2014.
21. Multimode Multiplication and Squaring Circuits (Assigned to: Hunter Larson)
K. E. Wires, M. J. Schulte, L. P. Marquette, and P. I. Balzola, "Combined Unsiged and Two's Complement Squarers," Proc. 33rd Asilomar Conf. Signals Systems and Computers, 1999, pp. 1215-1219.
22. Design of Cubing Circuits (Assigned to: )
B. N. K. Reddy, B. Seetharamulu, G. S. Krishna, and B. V. Vani, "An FPGA and ASIC Implementation of Cubing Architecture," Wireless Personal Communications, Vol. 125 No. 4, pp. 3379-3391, 2022.
E. Vassalos and D. Bakalis, "On the Design of Modulo 2^n – 1 Cubing Units," Proc. 23rd ACM Great Lakes Symp. VLSI, 2013, pp. 251-256.
23. Generalized Recursive Multipliers Built of Possibly Nonsquare Modules (Assigned to: )
B. Parhami, "A Theoretical Analysis of Square versus Rectangular Component Multipliers in Recursive Multiplication,"
Proc. 50th Asilomar Conf. Signals, Systems, and Computers, 2016, pp. 157-161.
S. Mazahir, O. Hasan, R. Hafiz, and M. Shafique, "Probabilistic Error Analysis of Approximate Recursive Multipliers," IEEE Trans. Computers, Vol. 66, No. 11, pp. 1982-1990, 2017.
24. Merged Arithmetic: The Case of Add-Multiply-Add Circuits (Assigned to: )
E. Hakkennes and S. Vassiliadis, "Multimedia Execution Hardware Accelerator," J. VLSI Signal Processing, Vol. 28, No. 3, pp. 221-234, July 2001.
K. A. Feiste and E. E. Swartzlander, "Merged Arithmetic Revisited," Proc. IEEE Workshop on Signal Processing Systems, 1997, pp. 212-221.
25. A Comparison of Hardware Multipliers Used in Microprocessors (Assigned to: )
G. Colon-Bonet and P. Winterrowd, "Multiplier Evolution: A Family of Multiplier VLSI Implementations," Computer J., Vol. 51, No. 5, pp. 585-594, 2008.
26. A Survey of Multiplier Circuits in Digital Signal Processors (Assigned to: )
J. M. Jou, S. R. Kuang, and R. D. Chen, "Design of Low-Error Fixed-Width Multipliers for
DSP Applications," IEEE Trans. Circuits and Systems II, Vol. 46, pp. 836-842, June 1999.
S. J. Jou, M.-H. Tsai, and Y.-L. Tsao, "Low-Error Reduced-Width Booth Multipliers for DSP Applications," IEEE Trans. Circuits and Systeme I, Vol. 50, No. 11, pp. 1470-1474, November 2003.
Topics for Part IV of the Textbook: Division
27. Radix-16 SRT Division: Algorithm and Implementations (Assigned to: )
[Intel's] New Radix-16 Divider
28. A Survey of the Applications of Reciprocation and Square-Rooting (Assigned to: )
29. Combinational Circuits for Fast Approximate Reciprocation (Assigned to: )
P.-M. Seidel, "High-Speed Redundant Reciprocal Approximation," Integration, The VLSI J., Vol. 28, No. 1, pp. 1-12, September 1999.
A. Habegger, A. Stahel, J. Goette, and M. Jacomet, "An Efficient Hardware Implementation for a Reciprocal Unit." Proc. 5th IEEE Int'l Symp. Electronic Design, Test & Applications, 2010, pp. 183-187.
30. On-the-Fly Conversion of Redundant Quotients into Nonredundant Form (Assigned to: )
31. Practical Hardware Implementation of Montgomery Modular Multiplication (Assigned to: )
S. Fatemi, M. Zare, A. F. Khavari, and M. Maymandi-Nejad, "Efficient Implementation of Digit-Serial Montgomery Modular Multiplier Architecture," IET Circuits, Devices & Systems, Vol. 13, No. 7, pp. 942-949, 2019.
32. Convergence Division with Faster-than-Quadratic Convergence (Assigned: )
I. Kong and E. E. Swartzlander, "A Goldschmidt Division Method with Faster than Quadratic Convergence," IEEE Trans. VLSI Systems, Vol. 19, No. 4, pp. 696-700, April 2011.
G. Paim, P. Marques, E. Costa, S. Almeida, and S. Bampi, "Improved Goldschmidt Algorithm for Fast and Energy-Efficient Fixed-Point Divider," Proc. 24th IEEE Int'l Conf. Electronics, Circuits and Systems, 2017, pp. 482-485.
Topics for Part V of the Textbook: Real Arithmetic
33. History of Floating-Point Number Representation Formats and Associated Standards (Assigned to: )
34. Level-Index Number Rerpesentation and Arithmetic (Assigned to: )
35. Sign/Logarithmic Arithmetic and the European Logarithmic Microprocessor (Assigned to: )
J. N. Coleman, et al., "The European Logarithmic Microprocessor," IEEE Trans. Computers, Vol. 57, No. 4, pp. 532-546, April 2008.
J. N. Coleman, E. I. Chester, C. I. Softley, and J. Kadlec, "Arithmetic on the European Logarithmic Microprocessor," IEEE Trans. Computers, Vol. 49, No. 7, pp. 702-715, July 2000.
36. Residue Logarithmic Number Representation and Arithmetic (Assigned to: )
37. Accurate Summation of Sets of Floating-Point Numbers (Assigned to: )
A. Eisinberg and G. Fedele, "Accurate Floating-Point Summation: A New Approach," Applied Mathematics and Computation, Vol. 189, pp. 410-424, 2007.
T. Ogita, S. M. Rump, and S. Oishi, "Accurate Sum and Dot Product," SIAM J. Scientific Computing, Vol. 26 , No. 6, pp. 1955-1988, 2005.
38. Multiprecision Arithmetic on Media Processors (Assigned to: )
39. Implementing Arithmetic Functions with Interval Arithmetic (Assigned to: )
U. Kulisch, "Mathematics and Speed for Interval Arithmetic: A Complement to IEEE 1788," ACM TOMS, Vol. 45, No. 1, March 2019, pp. 5:1-5:22. [https://doi.org/10.1145/3264448]
Topics for Part VI of the Textbook: Function Evaluation
40. Combinational Circuits for Fast Approximate Square-Rooting (Assigned to: )
41. Cube Roots: Hardware Algorithms and Applications (Assigned to: )
A. Pineiro, J. D. Bruguera, F. Lamberti, and P. Montuschi, "A Radix-2 Digit-by-Digit Architecture for Cube Root," IEEE Trans. Computers, Vol. 57, No. 4, pp. 562-566, April 2008.
Cube-Roots via Newton-Raphson Method
42. Argument Reduction for Faster, More Accurate Function Evaluation (Assigned to: )
S. Boldo, M. Daumas, and R.-C. Li, "Formally Verified Argument Reduction with a Fused Multiply-Add," IEEE Trans. Computers I, Vol. 58, No. 8, pp. 1139-1145, August 2009.
N. Brisebarre, et al., "A New Range-Reduction Algorithm," IEEE Trans. Computers, Vol. 54, No. 3, pp. 331-339, March 2005.
43. Function Evaluation by Piecewise Linear Approximation (Assigned to: )
N. Takagi, "Powering by a Table Look-Up and A Multiplication with Operand Modification," IEEE Trans. Computers, Vol. 47, No. 11, pp. 1216-1222, Nov. 1998.
O. Gustafsson and K. Johanson, "Multiplierless Piecewise Linear Approximation of Elementary Functions," Proc. 40th Asilomar Conf. Signals, Systems, and Computers, October 2006.
44. Smaller Lookup Tables by Exploiting Symmetry and Nonuniform Segmentation (Assigned to: Torin Schlunk)
D.-U Lee, R. C. C. Cheung, W. Luk, and J. D. Villasenor, "Hierarchical Segmentation for Hardware Function Evaluation," IEEE Trans. VLSI Systems, Vol. 17, No. 1, pp. 103-116, January 2009.
T. Sasao, S. Nagayama, and J. T. Butler, "Numerical Function Generators Using LUT Cascades," IEEE Trans. Computers, Vol. 56, No. 6, pp. 826-838, June 2007.
Topics for Part VII of the Textbook: Implementation Topics
45. Pipelined Arithmetic in Vector Supercomputers (Assigned to: )
46. Online or Digit-Pipelined Arithmetic with Carry-Save Operands (Assigned to: )
47. On-the-Fly Arithmetic Converters as Finite Automata (Assigned to: )
N. Pippenger, "On-the-Fly Algorithms and Sequential Machines," IEEE Trans. Computers, Vol. 60, No. 9, pp. 1372-1375, September 2011.
C. Frougny, "On-the-Fly Algorithms and Sequential machines," IEEE Trans. Computers, Vol. 49, No. 8, pp. 859-863, 2000.
48. Low-Power Full-Adder Cells and Their Applications (Assigned to: )
K. Navi, et al., "A Novel Low-Power Full-Adder Cell for Low Voltage," Integration, the VLSI J., Vol. 42, No. 4, pp. 457-467, September 2009.
M. Aguirre-Hernandez and M. Linares-Aranda, "CMOS Full-Adders for Energy-Efficient Arithmetic Applications," IEEE Trans. VLSI Systems, Vol. 19, No. 4, pp. 718-721, April 2011.
49. Low-Power Design Techniques for Multipliers (Assigned to: Parth Kulkarni)
I. S. Abu-Khater, A. Bellaouar, and M. I. Elmasry, "Circuit Techniques for CMOS Low-Power
High-Performance Multipliers," IEEE J. Solid-State Circuits, Vol. 31, pp. 1535-1546, October 1996.
S. S. Mahant-Shetti, P. T. Balsara, and C. Lemonds, "High Performance Low Power Array
Multiplier Using Temporal Tiling," IEEE Trans. VLSI Systems, Vol. 7, No. 1, pp. 121-124, March 1999.
50. Dedicated Hardware Multipliers on FPGA Chips (Assigned to: )
Using Embedded Multipliers in Spartan-3 FPGAs
51. Building Wider Multipliers from Embedded FPGA Multipliers (Assigned to: )
S. Gao, D. Al-Khalili, and N. Chabini, "Efficient Realization of Large Size Two's Complement Multipliers Using Embedded Blocks in FPGAs," Circuits, Systems, and Signal Processing, Vol. 27, No. 5, pp. 713-731, October 2008.
J.-L. Beuchat and A. Tisserand, "Small Multiplier Based Multiplication and Division Operators for Virtex-II Devices," Proc. 12th Int'l Conf. Field-Programmable Logic and Applications, 2002, pp. 513-522.
52. Augmenting FPGAs for Faster Arithmetic Operations (Assigned to: Minghe Li)
H. Parandeh-Afshar, A. K. Verma, P. Brisk, and P. Ienne, "Improving FPGA Performance for Carry-Save Arithmetic," IEEE Trans. VLSI Systems, Vol. 18, No. 4, pp. 578-590, April 2010.
K. E. Murray, J. Luu, M. J. Walker, et al., "Optimizing FPGA Logic Block Architectures for Arithmetic," IEEE Trans. VLSI Systems, Vol. 28, No. 6, pp. 1378-1391, 2020.
General Research Topics Spanning Multiple Parts
53. A Survey of Arithmetic Circuits in Electronic Scientific Calculators (Assigned to: Keshav Taneja)
G. R. Rising, Inside Your Calculator: From Simple Programs to Significant Insights, Wiley, 2007.
H.-J. Bohm, "Small-Data Computing: Correct Calculator Arithmetic," Communications of the ACM, Vol. 60, No. 8, pp. 44-49, August 2017.
54. Arithmetic in Early Supercomputers: IBM System/360 Model 91 and CDC 6600 (Assigned to: )
55. Arithmetic and Energy Economy Provisions in IBM Blue Gene/L Parallel Supercomputer (Assigned to: Yicheng Qin)
J. Lorenz, S. Kral, F. Franchetti, and C.W. Ueberhuber, "Vectorization Techniques for the Blue Gene/L Double FPU," IBM J. Research and Development, Vol. 49, Nos. 2/3, pp. 437-446, March/May 2005.
S. Chatterjee, et al., "Design and Exploitation of a High-Performance SIMD Floating-Point Unit for Blue Gene/L," IBM J. Research and Development, Vol. 49, Nos. 2/3, pp. 377-391, March/May 2005.
56. Implementation of Arithmetic Operations in Graphics Processors (Assigned to: )
D. De Caro, N. Petra, and A. G. M. Strollo, "High-Performance Special Function Unit for Programmable 3-D Graphic Processors," IEEE Trans. Circuits and Systems I, Vol. 56, No. 9, pp. 1968-1978, September 2009.
D. Blythe, "Rise of the Graphics Processor," Proc. IEEE, Vol. 96, No. 5, pp. 761-778, May 2008.
57. Arithmetic in a Near-Pixel SIMD Architecture for 3D Stacked Chips (Assigned to: Shaoqian Zhou)
B. Pfundt, M. Reichenbach, C. Soll, and D. Fey, "Novel Image Processing Architecture for 3D Integrated Circuits," PARS-Mitteilungen, Vol. 32, No. 1, 2015.
S. Chevobbe, M. Lepecq, K. Benchehida, M. Darouich, T. Dombek, F. Guellec, and L. Millet, "A Versatile 3D Stacked Vision Chip with Massively Parallel Processing Enabling Low Latency Image Analysis," Proc. Int'l Image Sensor Workshop, June 2019.
58. Implementation of Arithmetic Operations in Tensor Processing Units (Assigned to: Manan Gupta)
N. Jouppi, C. Young, N. Patil, and D. Patterson, D., "Motivation for and Evaluation of the First Tensor Processing Unit, IEEE Micro, Vol. 38, No. 3, 2018, pp. 10-19.
59. Number Crunching for Computer Games: History and Techniques (Assigned to: Harim Choe)
60. Arithmetic Operations for Elliptic Curve Cryptography (Assigned to: )
C. K. Koc (ed.), Cryptographic Engineering, Springer, 2009.
S. Kumar, Elliptic Curve Cryptography for Constrained Devices, VDM Verlag, 2008.
J. Solinas, "Generalized Mersenne numbers," Tech. Report CORR 99-39, Dept. C&O, U. Waterloo, 1999.
61. Implementation of Ultrahigh-Precision Arithmetic on Parallel Computers (Assigned to: )
D. Takahashi, "Parallel Implementation of Multiple-Precision Arithmetic and 2,576,980,370,000 Decimal Digits of Pi Calculation," Parallel Computing, Vol. 36, No. 8, pp. 439-448, August 2010.
62. Comparing Synchronous and Asynchronous Arithmetic Circuits (Assigned to: )
B. Pandey, J. Yadav, Y. K. Singh, and P. Swarnkar, "Energy Efficency of Asynchronous and Synchronous VLSI Circuit on 40nm and 90nm FPGA," Proc. Int'l Conf. Energy Efficient Technologies for Sustainability, 2013, pp. 57-60.
O. C. Akgun and Y. Leblebici, "Energy Efficiency Comparison of Asynchronous and Synchronous Circuits Operating in the Sub-Threshold Regime, J. Low Power Electronics, Vol. 4, No. 3, pp. 320-336, 2008.
63. Implementing Arithmetic Operations with Neuronlike Hardware Elements (Assigned to: Dominic Zboyan)
Neuronal Arithmetic: https://pmc.ncbi.nlm.nih.gov/articles/PMC4750293/
The Algebra of Neurons: https://www.mpg.de/18314224/0221-psy-the-algebra-of-neurons-155111-x
Math Neurons Identified in the Brain: https://www.sciencedaily.com/releases/2022/02/220214121241.htm
Owlish Neurons Do Advanced Math: https://www.science.org/content/article/owlish-neurons-do-advanced-math
64. Number Storage and Arithmetic with DNA (Assigned to: )
A. K. George, I. O. Kunnummal, L. Alazzawi, and H. Singh, "Design of DNA Digital Circuits," IEEE Potentials, March/April 2020, pp. 35-40.
65. Computer Arithmetic with Emerging Technologies (Assigned to: )
G. Bourianoff, "The Future of Nanocomputing," IEEE Computer, Vol. 36, No. 8, pp. 44-53, August 2003.
Y. Brun, "Arithmetic Computation in the Tile Assembly Model: Addition and Multiplication," Theoretical Computer Science, Vol. 378, No. 1, pp. 17-31, June 2007.
G. Jaberipur, B. Parhami, and D. Abedi, "Adapting Computer Arithmetic Structures to Sustainable Supercomputing in Low-Power, Majority-Logic Nanotechnologies," IEEE Trans. Sustainable Computing, Vol. 3, No. 4, pp. 262-273, October-December 2018.
66. Number Representation and Arithmetic for Machine Learning (Assigned to: Cameron Barrett)
67. A Comparative Evaluation of Open-Source GPU Architectures (Assigned to: Brandon Lee)
R. Balasubramanian et al., "Enabling GPGPU Low-Level Hardware Explorations with MIAOW: An Open-Source RTL Implementation of a GPGPU," ACM Trans. Architecture and Code Optimization, Vol. 12, No. 2, Article 21, 2015
Poster Presentation Tips
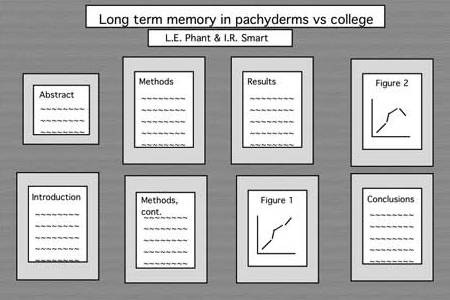
Here are some guidelines for preparing your research poster. The idea of the poster is to present your research results and conclusions thus far, get oral feedback during the session from the instructor and your peers, and to provide the instructor with something to comment on before your final report is due. Please send a PDF copy of the poster via e-mail by midnight on the poster presentation day.
Posters prepared for conferences must be colorful and eye-catching, as they are typically competing with dozens of other posters for the attendees' attention. Here is an example of a conference poster. Such posters are often mounted on a colored cardboard base, even if the pages themselves are standard PowerPoint slides. In our case, you should aim for a "plain" poster (loose sheets, to be taped to the wall in our classroom) that conveys your message in a simple and direct way. Eight to 10 pages, each resembling a PowerPoint slide, would be an appropriate goal. You can organize the pages into 2 x 4 (2 columns, 4 rows), 2 x 5, or 3 x 3 array on the wall. The top two of these might contain the project title, your name, course name and number, and a very short (50-word) abstract. The final two can perhaps contain your conclusions and directions for further work (including work that does not appear in the poster, but will be included in your research report). The rest will contain brief description of ideas, with emphasis on diagrams, graphs, tables, and the like, rather than text which is very difficult to absorb for a visitor in a very limited time span.
Grade Statistics
HW1 grades (out of 40): Range [22, 40], Mean = 35, Median = 36, SD = 4.7
HW2 grades (out of 35): Range [26, 35], Mean = 33, Median = 33, SD = 2.1
HW3 grades (out of 65): Range [52, 65], Mean = 61, Median = 62, SD = 3.6
HW4 grades (out of 60): Range [45, 60], Mean = 54, Median = 54, SD = 3.8
Overall HW grades (%): Range [82, 97], Mean = 92, Median = 92, SD = 4.0
Research paper grade (%): Range = [75, 100], Mean = 90, Median = 93, SD = 8.1
Course letter grades: Range = [B, A], Mean = 3.58, Median = A–
References
Primary textbook (required):
Parhami, Computer Arithmetic: Algorithms and Hardware Designs, Oxford, 2nd ed., 2010.
Verilog descriptions of arithmetic circuits (recommended):
This course does not involve a lab component or implementation projects. For those interested in pursuing practical circuit implementations, the following book may be useful:
Cavanagh, Computer Arithmetic and Verilog HDL Fundamentals, CRC Press, 2010.
Other useful books (not required):
Brent/Zimmermann, Modern Computer Arithmetic, Cambridge, 2011
Deschamps/Bioul/Sutter, Synthesis of Arithmetic Circuits: ... , Wiley, 2006 (TK7895.A65D47)
Ercegovac/Lang, Digital Arithmetic, Morgan Kaufmann, 2004 (QA76.9.C62E73)
Ercegovac/Lang, Division and Square Root: ... , Kluwer, 1994 (QA76.9.C62E73)
Knuth, The Art of Computer Programming: Seminumerical Algorithms, Wiley, 1981 (QA76.6.K64 vol 2)
Kulisch/Miranker, Computer Arithmetic in Theory and Practice, Academic Press, 1981 (QA162.K84)
Koren, Computer Arithmetic Algorithms, 2nd ed., A K Peters, 2002 (QA76.9.C62K67)
Muller, Elementary Functions: Algorithms and Implementation, Birkhauser, 2006 (QA331.M866)
Muller et al., Handobook of Floating-Point Arithmetic, Birkhauser, 2010
Oklobdzija, High-Performance System Design, IEEE Press, 1999 (TK7871.99.M44037)
Omondi, Computer Arithmetic Systems: ... , Prentice-Hall, 1994 (QA76.9.C62O46)
Omondi, Computer-Hardware Evaluation of Mathematical Functions, Imperial College Press, 2015
Swartzlander, Computer Arithmetic, vols. 1-2, IEEE Computer Society Press, 1990 (QA76.6.C633)
Waser/Flynn, Intro. Arithmetic for Digital Systems Designers, HR&W, 1982 (TK7895.A65W37.1982)
Research resources:
Proc. IEEE Symp. Computer Arithmetic, 1969, 72, 75 78, 81 and subsequent odd years; beginning with ARITH-23 in July 2016, the conference became an annual event.
On-line proceedings for IEEE Symp. Computer Arithmetic, 1969-2019
IEEE Trans. Computers, particularly special issues/sections on computer arithmetic: 8/1970, 6/1973, 7/1977, 4/1983, 8/1990, 8/1992, 8/1994, 7/1998, 7/2000, 3/2005, 2/2009, 2/2011, 8/2012, 8/2014, 12/2017, 7/2019
UCSB library's electronic journals, collections, and other resources
Miscellaneous Information
Motivation: Computer arithmetic is a subfield of digital computer organization. It deals with the hardware realization of arithmetic functions to support various computer architectures as well as with arithmetic algorithms for firmware/software implementation. A major thrust of digital computer arithmetic is the design of hardware algorithms and circuits to enhance the speed of various numeric operations. Thus much of what is presented in this course complements the architectural and algorithmic speedup techniques covered as part of the advanced computer architecture (ECE 254A/B/C) sequence.
Catalog entry: 252B. Computer Arithmetic. (4) PARHAMI. Prerequisites: ECE 152A-B (Changing to ECE 154A). Lecture, 4 hours. Standard and unconventional number representations. Design of fast two-operand and multioperand adders. High-speed multiplication and division algorithms. Floating-point numbers, algorithms, and errors. Hardware algorithms for function evaluation. Pipelined, digit-serial and fault-tolerant arithmetic processors.
History: Professor Parhami took over the teaching of ECE 252B from the late Dr. James Howard in the winter quarter of 1989. By covering sequential machines,
computer arithmetic, and advanced microprocessor-based design, the graduate course sequence ECE 252A/B/C was meant to provide a firm foundation in the theories and techniques of advanced digital design. During the first few offerings of ECE 252B, Professor Parhami gradually modified the content to increase both its coverage and research orientation (the now-discontinued ECE 252A & 252C underwent similar transformations by Professor Kwang-Ting Cheng and Professor Parhami, respectively). In 2000, based on a decade of experience in teaching computer arithmetic, Professor Parhami published a reference volume and graduate-level textbook, Computer Arithmetic: Algorithms and Hardware Designs (Oxford Univ. Press), which is being used at many universities worldwide. The 2nd edition of this textbook appeared in 2010.
Offering of ECE 252B in spring 2024
Offering of ECE 252B in spring 2023
Offering of ECE 252B in spring 2021
Offering of ECE 252B in spring 2020
Offering of ECE 252B in spring 2019
Offering of ECE 252B in spring 2018
Offering of ECE 252B in spring 2017
Offering of ECE 252B in spring 2016 (PDF file)
Offering of ECE 252B in spring 2015 (PDF file)
Offering of ECE 252B in spring 2014 (PDF file)
Offering of ECE 252B in spring 2013 (PDF file)
Offering of ECE 252B in spring 2012 (PDF file)
Offering of ECE 252B in spring 2011 (PDF file)
Offering of ECE 252B in spring 2010 (PDF file)
Offering of ECE 252B in spring 2009 (PDF file)
Offerings of ECE 252B from 2000 to 2008 (PDF file)