Hybrid and Switched Systems
ECE229 — Fall 2005
Announcements
Posted on ![]()
Course description
|
|
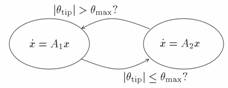
As computers, digital networks, and embedded systems become ubiquitous and increasingly complex, one needs to understand the coupling between logic-based components and continuous physical systems. This prompted a shift in the standard control paradigm—in which dynamical systems were typically described by differential or difference equations—to allow the modeling, analysis, and design of systems that combine continuous dynamics with discrete logic. This new paradigm is called hybrid control.
|
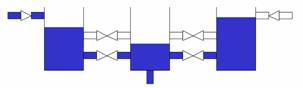
multiple-tank |
This course provides an
introduction to hybrid control. We start by presenting a modeling framework for hybrid systems that combines elements from
automata theory and differential equations. The students
are then guided through a set of techniques that can be used to analyze and design hybrid control systems.
The course also includes an overview of simulation tools for hybrid systems with
emphasis on Simulink/Stateflow, SHIFT, and Modelica.
|
transmission
|
In the last part of the course, we cover several fundamental applications of hybrid control. These include the modeling of communication networks, networked control systems, the modeling of bio-chemical reactions, the control of nonlinear systems that cannot be stabilized by continuous control laws, the control of systems with large uncertainty using logic-based supervisors, etc.
The course is essentially self-contained and the students are only expected to be familiar with linear algebra and basic differential equations.
Further information (including a detailed syllabus) is available on the web at:
http://www.ece.ucsb.edu/~hespanha/ece229/
This course was
developed with support from the National Science Foundation.
Prerequisites
Consent of instructor. This
course is open to
Recommended preparation: The
students should be proficient in linear algebra and basic differential
equations (at the level of MATH5A-C) and some scientific programming language
(e.g., MATLAB). Basic knowledge of controls concepts (at the level of ECE147A)
is helpful but not essential.
Instructor
João P. Hespanha (hespanha at ece.ucsb.edu),
phone:
Office hours: Please email or phone in advance to schedule an appointment.
Textbook
There is no recommended textbook for the course. Most of the material taught is covered by the following references:
[1] A. van der Schaft and H. Schumacher. An Introduction to Hybrid Dynamical Systems. Lecture Notes in Control and Information Sciences 251, Springer-Verlag, 2000.
[2] D.
Liberzon. Switching in Systems and
Control. Systems & Control: Foundations and Applications series.
Birkhauser,
[3]
[4]
Other papers and notes will also be posted in the course’s webpage to complement the lectures. See References below and right-most column of the Syllabus.
Assessment format
Homeworks – 40% (7-8 assignments)
Final Project – 60% (one-page project proposal is due on Oct 25th, in-class presentation)
Projects
The following two types of projects are possible in this course:
1. Solution of a research problem relevant to the student’s area of research
2. Independent study of a topic not covered in class (e.g., reading a paper or book chapter).
A few project ideas:
·
Modeling of network
protocols using hybrid systems [see this
paper]
·
Modeling of
networked control systems (could also have an experimental component) [see this survey]
·
Modeling of sensor
networks with stochastic hybrid systems
·
Controlling of
walking robots using hybrid systems [see these two papers GrizzleTAC, GrizzleCSM]
·
Modeling of
biological chemical reactions using stochastic hybrid systems [see this
paper].
·
Survey of
controllability and observability results for linear switched and hybrid
systems
·
Design of H-infinity
controllers for slowly-switched systems [see this paper]
·
Survey on optimal
control of hybrid systems
For more project ideas, students are encouraged to look into the proceedings of the Hybrid Systems: Computation and Control workshop. The full text of the proceedings is available online: HSCC'98, HSCC'99, HSCC'00, HSCC'01, HSCC'02, HSCC'03, HSCC’04, HSCC'05.
Detailed syllabus
The following is a tentative schedule for the course. As revisions are needed, they will be posted on the course's web page. The rightmost column of the schedule contains the recommended reading for the topics covered on each class. Students are strongly encouraged to read these and background materials prior to the class.
|
Class |
Content |
References |
|
Lec. #1 Sep 22 |
Introduction to switched control systems Examples: bouncing ball, thermostat, transmission system, inverted pendulum swing-up, multi-tank system, manufacturing systems, supervisory control. |
[1,27,28,29,4] lecture notes |
|
Lec. #2 Sep 27 |
Part I – Modeling & Simulation Formal models for hybrid systems: · Finite automata · Differential equations · Hybrid automata · Open hybrid automaton Nondeterministic vs. stochastic systems · Nondeterministic hybrid automata · Stochastic hybrid automata |
[1,8] lecture
notes |
|
Lec. #3 Sep 29 |
Trajectories of hybrid system · Solution to an hybrid system · Execution of an hybrid system Degeneracies · Finite-escape time · Chattering · Zeno trajectories · Non-continuous dependency on the initial-state |
[5,6,7] lecture
notes |
|
Lec. #4 Oct 4 |
Numerical simulation of hybrid automata · simulations of ODEs · zero-crossing detection Simulators · Simulink · Stateflow · SHIFT |
[9,10,11,12,13] lecture
notes Simulink/Stateflow
files
SHIFT
files
(untested) Modelica files |
|
Lec. #5 Oct 6 |
Simulators (cont.) · Modelica Part II – Analysis & Design Properties of hybrid automata · sequence properties (safety, liveness) · ensemble properties (stability) |
[14] lecture
notes |
|
Lec. #6 Oct 11 |
Safety/Reachability · transition systems · reachability algorithms · controller synthesis based on reachability |
[15, 16,17, 18] lecture
notes |
|
Lec. #7 Oct 13 |
Safety/Reachability (cont.) Lyapunov stability of ODEs · epsilon-delta and beta-function definitions · Lyapunov’s stability theorem · LaSalle’s invariance principle · Stability of linear systems |
[19] lecture
notes MATLAB files |
|
Oct 18 |
No class |
|
|
Oct 20 |
No class |
|
|
Lec. #8 Oct 25 Project proposal
due! |
Lyapunov stability of ODEs (cont.) Lyapunov stability of hybrid systems |
[3,19,20,21] lecture notes An alternative view |
|
Lec. #9 Oct 27 |
Analysis tools for hybrid systems: Impact maps · Fixed-point theorem · Stability of periodic solutions |
[3,23] lecture
notes Mathematica file |
|
Lec. #10 Nov 1 |
Impact maps (cont.) Switched systems · Linear Switched systems · Lyapunov stability of switched systems |
[2,3] lecture
notes |
|
Lec. #11 Nov 3 |
Stability under arbitrary switching · Instability caused by switching · Common Lyapunov function · Converse results · Algebraic conditions |
[2,3] lecture
notes MATLAB files |
|
Lec. #12 Nov 8 |
Controller realization for stable switching |
[24] lecture
notes |
|
Lec. #13 Nov 10 |
Stability under slow switching · Dwell-time switching · Average dwell-time · Stability under brief instabilities Stability under state-dependent switching · State dependent common Lyapunov function · Multiple Lyapunov functions · LaSalle’s invariance principle |
[3, 20,21,22] lecture
notes |
|
Lec. #14 Nov 15 |
Computational methods to construct multiple Lyapunov functions—Linear Matrix Inequalities (LMIs) Part III – Applications Vision-based control Systems that are not smoothly
stabilizable: |
[3,25] lecture
notes [34] |
|
Lec. #15 Nov 17 |
Modeling of network traffic |
[31] lecture notes |
|
Lec. #16 Nov 22 |
Stochastic hybrid systems · Communication networks · Networked control system · Bio-chemical reactions Supervisory control [4,30] |
[8,32] lecture
notes |
|
Nov 24 |
Thanksgiving
holiday |
|
|
Lec. #17 Nov 29 |
Student projects presentations |
|
|
Lec. #18 Dec 1 |
Student projects presentations |
|
References
Modeling
[5]
[6]
Jun Zhang, K. Johansson,
[7] K. Johansson,
[8]
Simulation
[9]
[10] The Mathworks Inc. Using Simulink (version 4), Nov. 2000.
[11] The Mathworks Inc. Stateflow User’s Guide (version 4), Sep. 2000.
[12] M.
Otter,
[13] Modelica Association. Modelica ™ — A Unified Object-Oriented Language for Physical Systems Modeling: Tutorial. Available at http://www.modelica.org/.
Reachability and other sequence
properties
[14]
Z. Manna and
[15]
[16]
[17]
[18]
Stability
[19] H. K. Khalil, Nonlinear Systems, 2nd edition, Prentice Hall, 1996.
[19a]
[20] M. Branicky. Multiple Lyapunov functions and other analysis tools for switched and hybrid systems. IEEE Trans. Automatic Control, 43(4):475-482, April 1998.
[21] H. Ye,
[22]
[23] J.
Grizzle, G. Abba,
[23a] C.
Chevallereau, Y. Aoustin, F. Plestan, E. Westervelt, C. Canudas-De-Wit, J.
Grizzle, RABBIT: a testbed for advanced
control theory, IEEE Control Systems
Magazine, 23(5):27—29, Oct. 2003. [pdf]
[24]
[25] S. Boyd,
[26] D. Liberzon, A. S. Morse, Basic problems in stability and design of switched systems. IEEE Control Systems Magazine, vol. 19, no. 5, pp. 59-70, Oct. 1999.
[27]
Applications
[28]
[29] K. Åström,
[30]
[31] S. Bohacek,
[32] J. Hespanha,
[33]
[34]
Homeworks
Modelica’s simulator dymola is available in the computer bradbury.ece.ucsb.edu and in the Linux workstations in the E1 lab. To get started do as follows:
1. Add the dymola directory to your PATH environment variable
In bradbury.ece.ucsb.edu, this can be done using the tcsh command
setenv
PATH /usr/local/dymola/bin:$PATH
In the
E1 lab, this can be done using the tcsh command
setenv
PATH /eci/dymola /bin:$PATH
2.
Start
the simulator using the command
dymola5
thermostat.mo
Documentation is available online and in references [12-13] above
|
Number |
Posted on |
Due date |
Exercises |
|
1 |
|
|
requires material from lectures #1 and #2 Solution will be provided in class |
|
2 |
|
|
requires material from lectures #2 and #3 |
|
3 |
|
|
requires material from lectures #4 and #5 |
|
4 |
|
|
requires material from lectures #6 and #9 |
|
5 |
|
|
requires material from lectures #11 and #12 |
|
6 |
2/8/04 |
2/19/04 |
|
|
7 |
2/14/04 |
2/26/04 |
|
|
8 |
2/22/04 |
3/15/04 |